도서 소개
어떤 질문을 하면 선생님을 당황하게 만들 수 있을까? 무슨 지식을 뽐내면 선생님의 입이 딱 벌어질까? 어떻게 하면 선생님이 내 실력을 인정하며 그저 고개를 끄덕이게 될까? 그런 경험을 한 번쯤 해 보고 싶다면 이 책을 꼭 읽어 보기 바란다.
이 책에는 선생님과 친구들 앞에서 수학 실력을 뽐낼 수 있는 여러 가지 비법들이 들어 있기 때문이다. 이 정도 수학 지식이라면 분명 선생님도 감탄할 수밖에 없을 것이다. 선생님도 놀라게 하는 수학에는 함수, 제곱근, 이차방정식, 삼각함수, 로그뿐만 아니라 기발하고 재미있는 다양한 수학 지식들이 직접 실험해볼 수 있는 예들과 함께 소개되고 있다.
내가 직접 해볼 수 있는 수학 증명들을 통해 개념과 원리를 이해해간다니 멋지지 않은가! 직접 해 보기 때문에 기억에도 오래오래 남을 것이다.
출판사 리뷰
재미있는 사실과 역사적 지식, 수많은 중요 수학 공식들과 그 증명까지! 전 세계에서 가장 수학적 성취가 높은 독일 고1 수준의 수학 개념과 수학으로 설명하는 물리 이야기!!어떤 질문을 하면 선생님을 당황하게 만들 수 있을까? 무슨 지식을 뽐내면 선생님의 입이 딱 벌어질까? 어떻게 하면 선생님이 내 실력을 인정하며 그저 고개를 끄덕이게 될까?
그런 경험을 한 번쯤 해 보고 싶다면 이 책을 꼭 읽어 보기 바란다. 이 책에는 선생님과 친구들 앞에서 수학 실력을 뽐낼 수 있는 여러 가지 비법들이 들어 있기 때문이다. 이 정도 수학 지식이라면 분명 선생님도 감탄할 수밖에 없을 것이다.
선생님도 놀라게 하는 수학에는 함수, 제곱근, 이차방정식, 삼각함수, 로그뿐만 아니라 기발하고 재미있는 다양한 수학 지식들이 직접 실험해볼 수 있는 예들과 함께 소개되고 있다.
내가 직접 해볼 수 있는 수학 증명들을 통해 개념과 원리를 이해해간다니 멋지지 않은가! 직접 해 보기 때문에 기억에도 오래오래 남을 것이다.
삼각형의 내각의 합이 늘 180°라는 말은 거짓말이다!
최고의 아름다움을 보장하는 황금비율
수학 천재 골탕 먹이기
음악과 수학의 상관관계
피보나치의 분수 표기법
분수를 싫어했던 수학자 스테빈
백분율과 분수 그리고 삼단논법
이차방정식의 근의 공식
π의 근삿값 구하기
탄젠트와 피타고라스의 정리
라플라스의 악마
주사위는 던져졌다!
확률 제로와 불가능은 동의어가 아니다!
부자가 돈을 딸 확률이 더 높은 이유
운이 좋은 사람 vs 운이 나쁜 사람
만사형통 로그 공식!
이 다양한 제목들처럼 선생님도 놀라게 하는 수학에서는 이각형이 어떻게 생겼는지, 자와 컴퍼스만 이용해서 주어진 원과 동일한 면적을 가진 정사각형을 그리는 게 왜 불가능한지, 복리複利의 위력이 얼마나 무시무시한지 등 똑똑해지고 싶은 친구들을 위한 수많은 수학 상식들이 들어 있다. 그러니 이 책을 읽고 직접 확인해 보며 누구보다 멋진 수학 지식을 자랑해 보길 바란다.

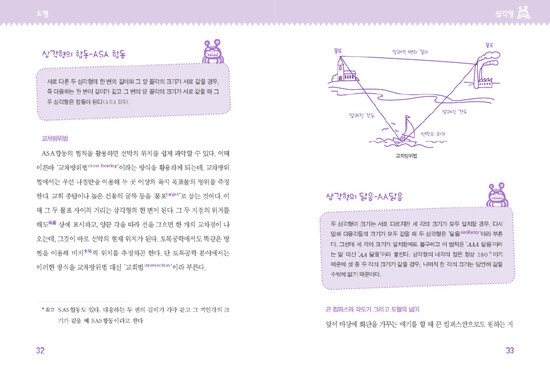






 삼각형의 내각의 합이 항상 180°인 것은 아니다?!
삼각형의 내각의 합이 항상 180°인 것은 아니다?!영국 작가 테리 프래쳇Terry Pratchett(1948년)은 삼각형의 내각의 합이 항상 180°라는 주장은 황새가 아이를 물어다 준다는 말만큼이나 근거 없는 낭설에 불과하다고 비판했다. 수학에 무지한 사람들에게나 통할 법한 거짓말에 불과하다는 뜻이었다. 실제로 삼각형의 내각의 합이 늘 180°라는 말은 거짓말이다! 평면 위에서는 해당 법칙이 진실일지 몰라도 구면 위에서는 적용되지 않는다. 구면 위에 놓인 삼각형의 내각의 합은 항상 180°보다 크다. 참고로 구면 위 삼각형의 면적은 구면과잉에 비례한다. ‘구면과잉spherical excess’이란 구면 위에 놓여 있는 다각형의 내각의 합과 평면 위에 놓여 있는 다각형의 내각의 합의 차이를 가리키는 말이다(가령 구면 삼각형의 세 각을 합한 것과 180° 외의 차. 이때 두 다각형의 변의 개수는 동일함).
구면과잉은 특히 토지 측량학이나 지도 제작 분야에서는 매우 중요하다. 구면과잉을 감안하지 않을 경우, 전반적으로 울퉁불퉁하면서 면적이 넓은 토지를 측량할 때, 혹은 해당 토지에 대한 지도를 제작할 때 오차가 커질 수밖에 없기 때문이다. 다시 말해, 입체 위에서 구면과잉을 감안하지 않을 경우 실제 면적과의 오차가 감당할 수 없을 만큼 커질 수도 있다는
뜻이다. 반면 측정 대상 토지가 비교적 평면에 가깝다면 구면과잉을 무시하고 이차원 위에서 면적을 구할 때와 동일한 방법을 활용해도 크게 문제되지 않는다.
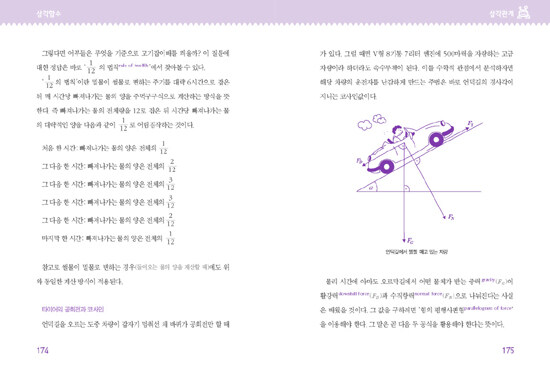
적분과 함수f(x)=ax+b의 함수 그래프 아래쪽의 넓이를 구하는 과정은 가장 간단한 형태의 적분 계산으로도 가능하다. ‘적분integral’은 함수의 계산 방식을 가리키는 말로써, 적분 공식에서는 ‘인테그랄’이라는 기호를 사용한다. 사실 인테그랄이라는 말만 들어도 무시무시한 공식부터 떠올리며 겁먹는 학생들이 많은데, 그 뒤에 숨은 원리는 그다지 무시무시하지 않다.
물론 고등학생이 되면 직선적분뿐 아니라 다양한 곡선에 관한 적분 계산도 배워야 하고, 그 계산은 솔직히 말해서 조금 복잡하고 어렵다. 하지만 적분의 가장 밑바탕이 되는 기본 원리는 앞서 사다리꼴의 면적을 구하는 과정과 동일하다.
목차
1. 도형 9
원 10 삼각형 27 각도 40
2. 좌표 51
좌표 52 함수 57
3. 소수 63
소수 64 소인수 71
4. 제곱근 75
제곱수 76 무리수 제곱근 86
5. 분수 109
분수 110 백분율 123
6. 이차방정식 131
포물선 132 이항식 137
제곱근 공식 140
7. 구 147
원 148 원기둥 156 구 160
8. 삼각함수 169
삼각관계 170 쌍곡선 186
9. 확률 189
통계적 확률 190 주관적 확률 196
조건부 확률 202
10. 로그 211
로그함수 그래프 212
로그의 종류 219
찾아보기 222










